JEE 2018 :: Physics (2018) :: Solved questions 2018

• Physics (2018) - Solved questions 2018

A telephonic communication service is working at carrier freequency of 10 GHz. Only 10% of it is utilised for transmission. How many telephonic channels can be transmitted simultaneously, if each channel requires a bandwidth of 5kHz?

Answer:

Explanation:

Only 10% of 10 GHz is utillised for transmission.

  $\therefore$      Band available for transmission

                        = $\frac{10}{100}\times 10 \times 10^{9}Hz =10^{9} Hz$

   Now, If there are n channels each using 5 kHz then,  $n \times 5\times 10^{3}=10^{9}$

       $\Rightarrow$                            $n =2\times 10^{5}$

The reading of the ammeter for a silicon diode in the given circuit is

Answer:

Explanation:

Key Idea Potential drop in a silicon diode in forward bias is around 0.7 V. In given circuit, potential drop across 200Ω resistor is

                  $     I= \frac{\triangle V_{net}}{R}=\frac{3-0.7}{200} $

    $ \Rightarrow$   I =0.0115A $ \Rightarrow$   I=11.5mA

If the series limit frequency of the Lyman series is v_L, the the series limit frequency of the Pfund series is 

Answer:

Explanation:

Key idea Series limit occurs in the transition n₂= $\infty$  to n₁= 1 in Lyman series and n₂= $\infty$  to n₁ =5 in pfund series. For Lyman series,

 $hv_{L}=13.6$      ..........(i)

  In pfund series

$hv_{p}=\frac{13.6}{5^{2}}$ ........(ii)

 From Eqs. (i) and (ii), we get

 $25hv_{p}=hv_{L}$

$\therefore$ $v_{p}=\frac{v_{L}}{25}$

The angular width of the central maximum in a single slit diffraction pattern is 60° .The width of the slit is 1μm. The slit illuminated by monochromatic plane waves. If another slit of same width is made near it, Young's fringes can be observed on a screen placed at a disance 50cm from the slits. If the observed fringe width is 1 cm, what is slit seperation distance? (i.e. distance between the centres of each slit).

Answer:

Explanation:

Angular width of differaction pattern=60°

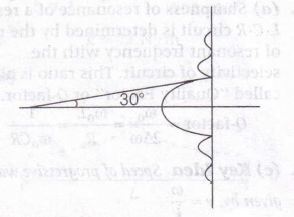
For first minima,

$\frac{a}{2}\sin\theta=\frac{\lambda}{2}$, [ here,a=10^-6m, θ=30°]

$\Rightarrow\lambda=10^{-6}\times \sin30^{0}\Rightarrow\lambda=\frac{10^{-6}}{2}m$

Now, in case of interference caused by bringing second slit,

$\therefore$    Fringe width, $\beta=\frac{\lambda D}{d}$

      [ here, 

$\lambda =\frac{10^{-6}}{2}m , \beta =1cm=\frac{1}{100}m,
d=?,and D=50cm=\frac{50}{100}m$ ]

So, $d=\frac{\lambda D}{\beta}=\frac{10^{-6}\times 50}{2\times \frac{1}{100}\times 100}=25\times 10^{-6}m$

or $d=25\mu m$

An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii r_e,r_p,rα is repectively, in a unifrom magnetic field B. The relation between r_e,r_p, r_α is>>

Answer:

Explanation:

From  $Bqv=\frac{mv^{2}}{r},$ we have

    $r=\frac{mv}{Bq}=\frac{\sqrt{2mK}}{Bq}$

     where,K is the kinetic energy

 As,  kinetic energies of particles are same ;

  $r\propto \frac{\sqrt{m}}{q}$

=   $r_{e}:r_{p}:r_{\alpha}=\frac{\sqrt{m}_{e}}{e}:\frac{\sqrt{m_{p}}}{e}:\frac{\sqrt{4m_{p}}}{2e}$

 Clearly,  $r_{p}=r_{\alpha} $ and $r_{e}$ , is least [ $\because m _{e}<m_{p}$ ]

  So,    $r_{p} =r_{\alpha}>r_{e}$

• Physics (2018) - Solved questions 2018